The goal of Reinforcement Learning
1. A scenario
Think of a video game character, like Mario, trying to get a high score. In reinforcement learning terms:
- State( $s$ ): A snapshot of the world. For Mario, it’s his position, the location of enemies, and position of coins.
- Action( $a$ ): What the agent can do. Mario can run_left, run_right, jump, or do_nothing.
- Policy ( $\pi_{\theta}(s,a)$ ): The agent’s strategy. Given Mario’s current state (e.g, a Goomba is nearby), the policy decides the probability of jumping vs running left vs running right.
- Reward ( $r(s,a)$ ): Feedback from the environment. Mario gets +100 points for grabbing a coin (a positive reward) and -1 life for hitting a Goomba (a negative reward).
- Trajectory ($\tau$): An entire episode (game) till the end with sequence of (state, action, reward). It’s like one full playthrough of a level:
(start, run_right, 0), (coin-above, jump, +100) (mid-air, do_nothing, 0)…. The state here is written in text, but it could be an image of the game.
In reinforcement learning (RL), our goal is to train an agent (e.g., Mario) to make optimal decisions (by learning good policy) by itself.
2. Deciding what actions to take in current state using policy
I like to think of policy as a strategy of the agent. A policy $\pi_\theta(s,a)$ takes the state of the world $s$ and outputs the likelihood of taking each possible action $a$; where $\theta$ is the parameters of the policy. If our policy network is a neural network then parameter $\theta$ would be weights and biases of the network.
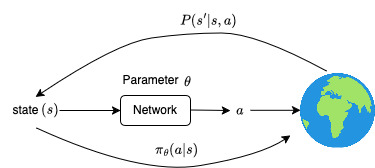
Reinforcement learning
Generally, we would like train the policy network in a way that high likelihood of any action means that the action is a ‘good’ action.
3. Interacting with the environment
When the robot takes an action $a$ in state $s$, the world/environment transitions to state $s’$ with a likelihood of $P(s’|s,a)$, and the robot gets a reward of $r(s,a)$. Imagine of this as: when Mario takes an action $a$ ($a$ = jump) in state $s$ ($s$ = Goomba approaches him), 90% of the time Mario reaches a state $s’$where Goomba is killed with positive reward, and 10% of the time, maybe because of slow response, Mario fails to kill Goomba and game is over with negative reward.
The agent (Mario) takes an action $a$ given by the policy $\pi_\theta(a | s)$ for every state $s$ to reach new state $s’$ until the game ends, generating an entire playthrough called a trajectory ($\tau$):
\[\tau = \{s_1, a_1, r_1, s_2, a_2, r_2, s_3, a_3, r_3, ...\}\]where $s_t, a_t, r_t$ are state, action, and reward at timestep $t$.
We can calculate the probability of our agent (Mario) generating this specific sequence of events if it follows policy $\pi_\theta$ using chain rule of probability as below:
The likelihood of this trajectory can be computed using the chain rule as below:
\[\begin{aligned}P_\theta(\tau) &= P_\theta(s_1,a_1,s_2,a_2,...) \\ &= P(s_1) P(a_1\|s_1)P(s_2\|s_1,a_1)P(a_2\|s_1,a_1,s_2)P(s_3\|s_1,a_1,s_2,a_2) \cdots \\ \end{aligned}\]According to the Markov property, the next state depends only on the current state and action: i.e., $P(s_{t+1}|s_t,a_t,s_{t-1},a_{t-1},\cdots) = P(s_{t+1}|s_t,a_t)$. Also, the policy depends only on the current state: i.e., $P(a_t|s_t,s_{t-1},a_{t-1},\cdots) = \pi_\theta(a_t|s_t)$.
Therefore, above equation can be written as:
\[\begin{aligned}P_\theta(\tau) &= P(s_1)\pi_\theta(a_1\|s_1)P(s_2\|s_1,a_1)\pi_\theta(a_2\|s2)P(s_3\|s_2,a_2) \cdots \\ &= P(s_1)\prod_{t=1}^T{\pi_\theta(a_t\|s_t) P(s_{t+1}\|s_t, a_t)} \\ \end{aligned}\]4. What makes this trajectory/episode good and bad?
Our Mario’s objective isn’t to get one coin, but to maximize the total score (reward) it gets till the end of the episode or game. The total score/reward $G(\tau)$ for one entire playthrough/episode (the trajectory $\tau)$ is the sum of all individual scores/rewards, written as:
\[G(\tau) = r1 + r2 + \cdots = \sum_{t=1}^Tr(s_t,a_t)\]Since total reward of the episode ultimately depends on all the actions taken at each timestep in the episode, we can say that the trajectory $\tau$ is good if it has high total reward $G(\tau)$ and bad if it has low total reward $G(\tau)$.
- If the episode was good (high $G(\tau)$ ): We want to see this kind of episode/trajectories more often, i.e, we need to increase $P_\theta(\tau)$ To make it more likely to happen again.
- If the episode was bad (less $G(\tau)$): We want to see this episode/trajectories less often, i.e., we need to decrease $P_\theta(\tau)$ to make it less likely to happen again.
Now, if we look at the equation of $P_\theta(\tau)$, we cannot simply increase or decrease $P_\theta(\tau)$. Our agent only has control over its policy $\pi_\theta(a_t|s_t)$ . The agent cannot change the starting state probabilities $P(s_1)$ or the rules of the environment $P(s_{t+1}|s_t,a_t)$. Therefore, the agent should adjust its policy parameters $\theta$ to change $\pi_\theta$ to increase or decrease the probability of actions taken during that episode depending on whether the episode was good (desirable) or bad (undesirable) respectively.
This simple, yet powerful, idea is the foundation of major family of RL algorithms called Policy Gradients. In these algorithms, high reward trajectories tells us “do more of that”, and low-reward trajectory tells us “do less of that”, by adjusting $\theta$ to push the action probabilities $\pi_\theta(a_t|s_t)$ in the desired direction.
5. The goal of Reinforcement Learning
Putting it all together, the objective of reinforcement learning is to find parameters $\theta$ that defines a policy $\pi_\theta$ so as to maximize the expected value of sum of reward if the robot follows that trajectory $\tau$. i.e.,
\[\theta^* = \argmax_\theta E_{\tau \sim P_\theta(\tau)}\Big[\sum_t r(s,a)\Big]\]In simple terms, we are trying to find the best possible strategy for our agent that, on average, gets highest possible return.