STATISTICS 01 - Fundamental concept of statistics
Random variable:
Each time you roll a dice, the outcome will be from 1 to 6. If we roll a dice 10 times, the probability of getting an one is 1/6. Here the combination of values and associated probability is a random variable. Here random doesn’t mean process is non deterministic, only that we lack information to compute the result. We don’t know what will happen except probabilistically.
The range of values that can occur is called the sample space. When rolling a die, sample space is {1,2,3,4,5,6}. For a coin, sample space is {H,T}. But remember, sample space is not unique. For example: sample space when rolling a die can be {odd, even} also. A sample space is valid as long as it covers all the possibilities and any single event is described by only one element.
In statistics, capital letters are used for random variables. So, we might say that \(X\) is the random variable representing die toss, or \(Y\) are the heights of the students in the class.
Probability Distribution
The probability distribution gives the probability for the random variable to take any value in a sample space. For example, for a die we can say that:
| Value | Probability |
|---|---|
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
we denote this distribution as \(p(x)\). So we can write this as;
\(P(X=4) = p(4) = \frac{1}{6}\)
\(P(X=x_k)\) is the notation for “the probability of \(X\) being \(x_k\)”.
To be a probability distribution, no probability can be less than 0, and sum of the probabilities for all the values must be equal to one.
import numpy as np
import kf_book.book_plots as book_plots
belief = np.array([1, 4, 2, 0, 8, 2, 2, 35, 4, 3, 2])
belief = belief / np.sum(belief)
with book_plots.figsize(y=2):
book_plots.bar_plot(belief)
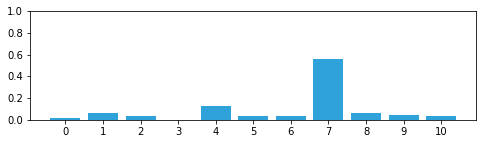
Since each position has probability between 0 to 1, and sum of all equals one, so this makes it a probability distribution
Mean, Median and Mode of Random variable
Average of data = Mean. So let,
\[X = \{1.8, 2.0, 1.7, 1.9, 1.6\}\]we compute the mean as
\[\mu = \frac{1.8 + 2.0 + 1.7 + 1.9 + 1.6}{5} = 1.8\]Number that occurs most often in data = Mode. So let,
\[Y = \{1, 2, 2, 2, 3, 4, 4, 4\}\]Mode of \(Y\) is 2 and 4 since it occurs three times. Since \(Y\) has two modes, we say it is a multimodal set. If it had only one mode, we would say it as unimodal set
Middle point of the set = Median. So let,
\[Z = \{1.8,2.0,1.7,1.9,1.6\}\]Median of \(Z\) is 1.8 because 1.8 is the third element of this set after being sorted - half of the values are below the median and hafl are above the median. In this case mean = median, but that is not generally true
Expected value of a random variable.
The expected value of a random variable is the average value it would have if we took an infinite number of sample of it and then averaged those samples together.
Let’s say we have \(x = [1,3,5]\) and each value is equally probable. We would expect x to have the average of 1,3, and 5 i.e 3.
But now, let’s say that 1 has 80% chance of occuring, 3 has 15% chance of occuring and 5 has only 5% chance of occuring. In this case, we compute expected value by multiplying each value of \(x\) by the percent chance of it occuring, and summing the result. So,
\[\mathbb E[X] = (1)(0.8) + (3)(0.15) + (5)(0.05) = 1.5\]where \(\mathbb E[x]\) is the notation for expected value of \(x\). Hence the formula for expected value of a random variable is
\[\mathbb E[X] = \sum_{i=1}^n p_ix_i\]total = 0
N = 10000000
for r in np.random.rand(N):
if r <= .80: total += 1
elif r < .95: total += 3
else: total += 5
print(total / N)
1.4997332
The expected value obtained is close to 1.5 which we have calculated mathematically above.
Variance of a Random variable
Until now, we know the average of the data, but we don’t know everything we might want to know. Let’s say we have three class of students which we label \(X,Y\) and \(Z\) and the data given in it is the height of the students.
\[X = [1.8, 2.0, 1.7, 1.9, 1.6]\] \[Y = [2.2, 1.5, 2.3, 1.7, 1.3]\] \[Z = [1.8, 1.8, 1.8, 1.8, 1.8]\]Using numpy we can see the mean of the data
X = [1.8, 2.0, 1.7, 1.9, 1.6]
Y = [2.2, 1.5, 2.3, 1.7, 1.3]
Z = [1.8, 1.8, 1.8, 1.8, 1.8]
print(np.mean(X), np.mean(Y), np.mean(Z))
1.8 1.8 1.8
The mean of each class is 1.8 meters, but we can see that there is much greater amount of variation in the heights in the second class than in the first class, and there is no variation in the third class.
The mean tells us something about the data, but not the whole story. We want to know how much variance there is between the height of the students.
The formula from the statistics for variance is:
\[\mathit{VAR}(X) = \mathbb E[(X - \mu)^2]\]using the formula for expected value, we get
\[\mathit{VAR}(X) = \frac{1}{n}\sum_{i=1}^n (x_i - \mu)^2\]Using numpy, we can see the variance of the data
print(f"{np.var(X):.2f} meters squared")
0.02 meters squared
This perhaps is quite hard to interpret. Heights are in meters, and variance is in meters squared. Thus we have a more commonly used measure called standard deviation which is defined as the squared root of variance.